About k-ε model convergence

This document is meant to give instructions for the resolution of the k-ε turbulence model but you could also use Prof. G. G. Katul's Matlab code to solve the model. His code is a dimensionless one. It used to require the replacement of some variable names related to turbulence length scales to run above the GNU-Octave interpreter.

---

The numerical simulation of a fully developped (uni-dimensional) boundary-layer in its steady state can be achieved rather easily. This document presents two "tricks", which are not necessarily obvious, but which seem definitely required for convergence. Here they are explained with the hope that they could be of some use to others.

The modelled budget equations in the one-dimensional case is simplified because no horizontal pressure gradient exist for the vertical problem, on average. You can refer to Sanz (2003) note to Boundary-Layer Meteorology for details. The numerical resolution proceeds in four steps:

1. Linearise the equations for U, k and ε . This linearisation consists in expressing the non linear terms, as well as the terms no related to the given unknown, either U, k or ε, as some functions of the terms at the previous iteration. When doing that, some care has to be taken with respect to the relative magnitude of the (implicit) terms dependent on the given unknwown vs. the non unknwown related (explicit) terms. An example for this principle is the viscous dissipation term in the modelled k budget equation. The equation below shows how the ε term in k budget should be represented

   

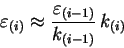
   where the subscript between parenthesis (i) refers to the calculated value at iteration number i. Omitting this "implicitisation" makes the ε term in k budget appear as a source of instability and may preclude the convergence of the numerical resolution. Note that in the ε budget equations, you can simplify the terms analogue to the k shear production ones. These latter terms are those involving the C_ε1 constant.

2. Discretise the linearised equations: express the derivatives as, most likely finite differences between flow properties at the discretisation points belonging to the vertical domain. The mixed order derivatives involved in the turbulent viscous diffusion should be consistently approximated by using the formal expression for the derivative of a product. The formula for the derivative of a product allows for the mixed order derivatives to be approximated from the discrete approximations for both first and second order derivatives.

3. Assemble the linear system of the discretised linearised equations with the boundary conditions. Also note that setting the boundary conditions is almost a topic in itself. You can contact me if you are interested in this topic. I can detail the implementation of the standard rough wall boundary conditions model here. I also look forward sharing views about the development of a boundary condition model for the transition between a rough surface and a dense canopy.

4. Solve the above mentionned linear system of equations for each unknown: U, k, and then ε. The turbulent kinematic viscosity (ν_t) being calculated from k and ε values, it can be updated after any update of k and after any update of ε, or after both k and ε have been updated. This latter solution seems to offer the more opportunities for parallelisation. In any case, does it seem, the observation of negative values for turbulence properties seems common experience, and the reason why a few authors used threshold &/or clipping techniques to avoid such negative values. A possibly proper solution could be found in the program TEAM, by P.G. Huang, B.E.Launder and M.A. Leschziner. It is illustrated by the equation below, using the same notation as above for successive iterates.

   

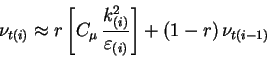
   This solution is to weight (under relax) the update of the ν_t value. The updated ν_t value is thereby assumed to lie between its calculated value at the current iterate and its value at the previous iterate. The weight value (r ~ 0.6) seems rather conservative but some cases might require a lower value. A similar under-relaxation procedure is recommended for any solved flow property, either U, k, or ε.